
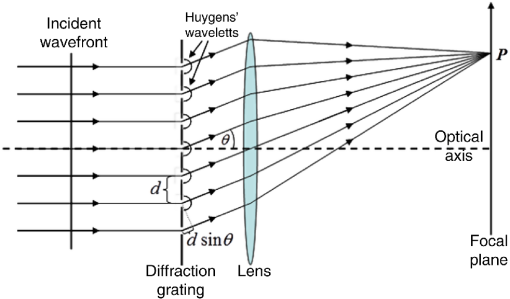
It is also shown that as the size increases only the peaks at higher 2 angles give good results, and if one uses peaks with 2 > 60° the limit for use of the Scherrer equation would go up to 1 µm. later formulated into the equation now known as the Abbe limit for resolution. well take the continuum limit and talk about slits. It is shown that for crystals with linear absorption coefficients below 2117.3 cm -1 the Scherrer equation is valid for crystallites with sizes up to 600 nm. The Rayleigh Criterion is a slightly refined formula based on Abbe’s diffraction limits: R 1.22 /NAobj+NAcond Where is the wavelength of light used to image a specimen. The various microscopy lateral resolution limits, of which the Rayleigh. On the other side of the screen, the wave equation must still be satisfied with boundary conditions. Notably, in contrast to all previous SSP.
#Diffraction limit equation full#
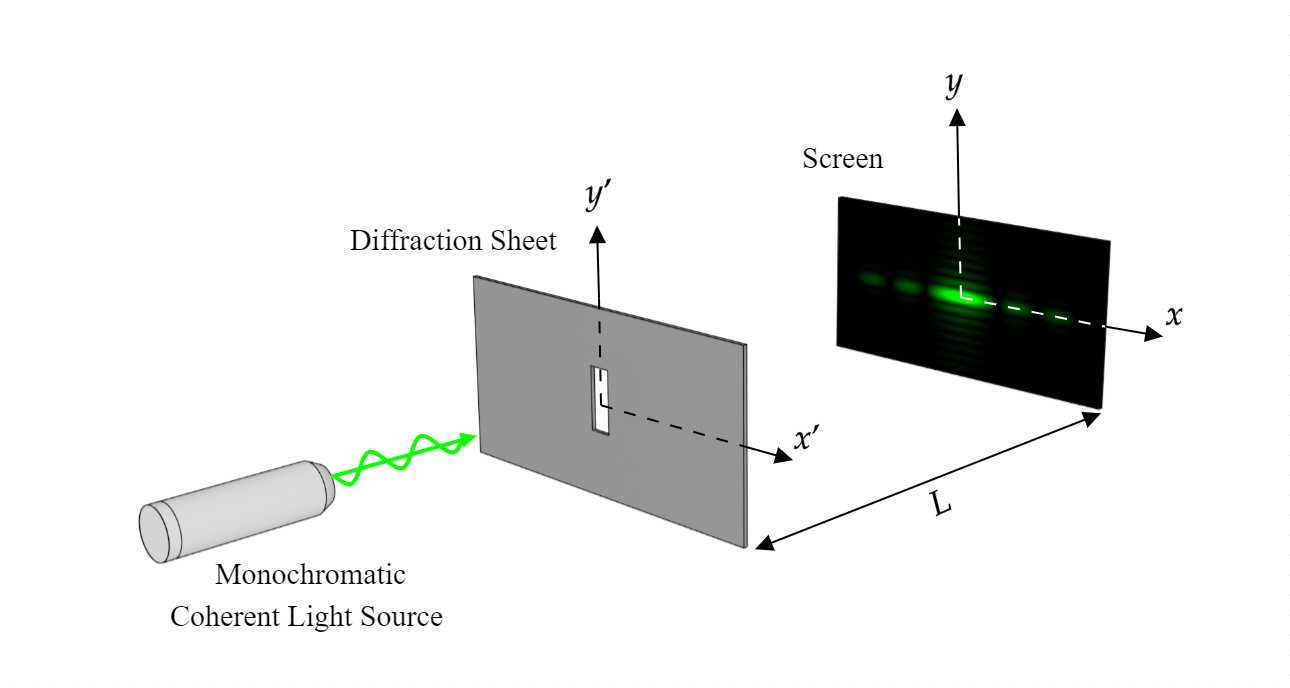
The full width at half-maximum is then extracted and the crystallite size is computed using the Scherrer equation. where Rk is the relative shift of the k-th mask, equation (1) takes the form of conventional scanning ptychography.
In this work, the diffraction peak profiles are calculated using the dynamical theory of X-ray diffraction for several Bragg reflections and crystallite sizes for Si, LaB 6 and CeO 2. 1.22 D The accepted criterion for determining the diffraction limit to resolution based on this angle was developed by Lord Rayleigh in the 19th century. The limit is basically a result of diffraction processes and the. Because of the appearance of polycrystalline materials with a high degree of crystalline perfection and large sizes, it is the authors' belief that it is important to establish the crystallite size limit for which the Scherrer equation can be applied. The numerical aperture (NA) and the resolution limit is schematically illustrated in figure 1. It is easy to show that Equation 15.15 applies to any reciprocalreceiver or transmitter of electromagnetic radiation anything from a telescope to an electric dipole antenna. For large and perfect crystals, it is more appropriate to use the dynamical theory of X-ray diffraction. 2, (15.14) orA2 (15.15) the area-solid angle product of a diffraction-limited beam is constant and equal to 2as the beam propagates. On both sides of central maximum diffraction fringes of unequal thickness are obtained. However, it is not clear if one can apply it to large crystallite sizes because its derivation is based on the kinematical theory of X-ray diffraction. The Scherrer equation is a widely used tool to determine the crystallite size of polycrystalline samples.


 0 kommentar(er)
0 kommentar(er)
